Fractais

Fractais (do latim fractus, fração, quebrado) são figuras da geometria não-Euclidiana.

A geometria fractal é o ramo da matemática que estuda as propriedades e comportamento dos fractais. Descreve muitas situações que não podem ser explicadas facilmente pela geometria clássica, e foram aplicadas em ciência, tecnologia e arte gerada por computador. As raízes conceituais dos fractais remontam a tentativas de medir o tamanho de objetos para os quais as definições tradicionais baseadas na geometria euclidiana falham.

Um fractal (anteriormente conhecido como curva monstro) é um objeto geométrico que pode ser dividido em partes, cada uma das quais semelhante ao objeto original. Diz-se que os fractais têm infinitos detalhes, são geralmente auto-similares e independem de escala. Em muitos casos um fractal pode ser gerado por um padrão repetido, tipicamente um processo recorrente ou iterativo.

O termo foi criado em 1975 por Benoît Mandelbrot, matemático francês nascido na Polónia, que descobriu a geometria fractal na década de 70 do século XX, a partir do adjetivo latino fractus, do verbo frangere, que significa quebrar.

Conjunto de Mandelbrot

Categorias de fractais

Aumento de 350 vezes do conjunto de Mandelbrot mostra os pequenos detalhes repetindo o conjunto inteiro.

Os fractais podem ser agrupados em três categorias principais. Estas categorias são determinadas pelo modo como o fractal é formado ou gerado:

• Sistema de funções iteradas — Estas possuem uma regras fixa de substituição geométrica. Conjunto de Cantor, tapete de Sierpinski, Sierpinski gasket, curva de Peano, floco de neve de Koch, curva do dragão de Harter-Heighway, T-Square, esponja de Menger, são alguns exemplos deste tipo de fractal.
• Fractais definidos por uma relação de recorrência em cada ponto do espaço (tal como o plano complexo). Exemplos deste tipo são o conjunto de Mandelbrot e o fractal de Lyapunov. Estes também são chamados de fractais de fuga do tempo.
• Fractais aleatórios, gerados por processos estocásticos ao invés de determinísticos, por exemplo, terrenos fractais e o vôo de Lévy.

Ainda, também podem ser classificados de acordo com sua auto-similaridade. Existem três tipos de auto-similaridade encontrados em fractais:

• Auto-similaridade exata: é a forma em que a auto-similaridade é mais marcante, evidente. O fractal é idêntico em diferentes escalas. Fractais gerados por sistemas de funções iterativas geralmente apresentam uma auto-similaridade exata.
• Quase-auto-similaridade: é uma forma mais solta de auto-similaridade. O fractal aparenta ser aproximadamente (mas não exatamente) idêntico em escalas diferentes. Fractais quase-auto-similares contém pequenas cópias do fractal inteiro de maneira distorcida ou degenerada. Fractais definidos por relações de recorrência são geralmente quase-auto-similares, mas não exatamente auto-similares.
• Auto-similaridade estatística: é a forma menos evidente de auto-similaridade. O fractal possui medidas númericas ou estatísticas que são preservadas em diferentes escalas. As definições de fractais geralmente implicam em alguma forma de auto-similaridade estatística (mesmo a dimensão fractal é uma medida numérica preservada em diferentes escalas). Fractais aleatórios são exemplos de fractais que possuem auto-similaridade estatística, mas não são exatamente nem quase auto-similares.

Entretanto, nem todos os objetos auto-similares são considerados fractais. Uma linha real (uma linha reta Euclidiana), por exemplo, é exatamente auto-similar, mas o argumento de que objetos Euclidianos são fractais é defendido por poucos. Mandelbrot argumentava que a definição de fractal deveria incluir não apenas fractais “verdadeiros” mas também objetos Euclidianos tradicionais, pois números irracionais em uma linha real representam propriedades complexas e não repetitivas.

Pelo fato do fractal possuir uma granulometria infinita, nenhum objeto natural pode sê-lo. Os objetos naturais podem exibir uma estrutura semelhante ao fractal, porém com uma estrutura de tamanho limitado.

Computação de um feto (samambaia)

Feto fractal

Um feto fractal pode ser gerado usando um sistema de funções iteradas começando com um ponto na origem e determinando iterativamente novos pontos a partir do resultado da aplicação aleatória de uma de 4 diferentes transformações de coordenadas:

Esta transformação, que é realizada apenas 1% das vezes, mapeia qualquer ponto para um ponto no segmento de recta mostrado a verde na figura.

Esta transformação, que é realizada apenas 7% das vezes, mapeia qualquer ponto dentro do rectângulo preto para um ponto dentro do rectângulo vermelho na figura.

Esta transformação, que é realizada apenas 7% das vezes, mapeia qualquer ponto dentro do rectângulo preto para um ponto dentro do rectângulo azul escuro na figura.

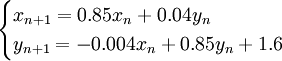
Esta transformação, que é realizada 85% das vezes, mapeia qualquer ponto dentro do rectângulo preto para um ponto dentro do rectângulo azul claro na figura.

A primeira transformações de coordenadas desenha o caule. A segunda, desenha a primeira folha da esquerda do feto. A terceira, desenha a primeira folha da direita do feto. E a quarta gera cópias sucessivas e garante que o todo é uma réplica maior de cada folha.